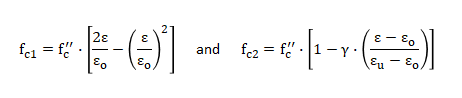IES ConcreteSection User's Guide
Analysis
A reinforced concrete section contains two dissimilar materials. Concrete has significant compressive strength and little or no tensile strength, whereas steel has similar strength in both tension and compression. As a result, simple equations are only available for two extreme states: pure compressive capacity and pure tension capacity. Any analysis of behavior between these states will require an iterative solution which satisfies principles of static equilibrium and compatibility of material strains. Regarding strains, it is assumed that plane sections remain plane and the reinforcement is bonded to the concrete so that both concrete and steel have the same strain at their interface (i.e. strain compatibility exists between the steel and the concrete). ConcreteSection solves this iterative process using the methods outlined in the reference at the end of this section.
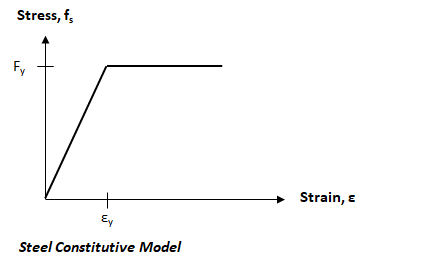
An elastic/perfectly plastic stress-strain relationship is used for tension and compression of the steel reinforcement in ConcreteSection.
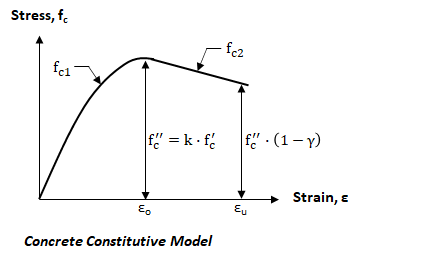
In ConcreteSection, the concrete is assumed to have no tensile capacity. In compression, the concrete stress-strain behavior is specified by parameters which include the concrete strain at maximum stress (eo), the ultimate concrete strain (eu), the maximum stress factor (k), and the confinement factor (g). The stress vs. strain diagram is shown below. The maximum concrete compressive stress (f"c) is obtained by multiplying the concrete compressive strength (f'c) by k. Note: f"c occurs when the compressive strain is eo. The compressive stress at the ultimate concrete strain is obtained by multiplying f"c by (1 - g). Increasing the confinement factor, g, reduces the effect of confinement on the section. The values for eo, eu, k, and g can be manually adjusted in ConcreteSection. The equations of the two lines shown below are as follows:
